The Centre for Vision Research
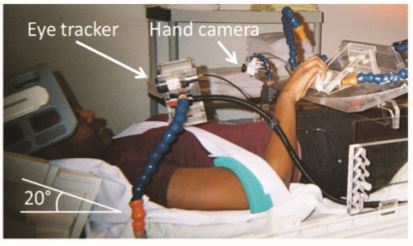
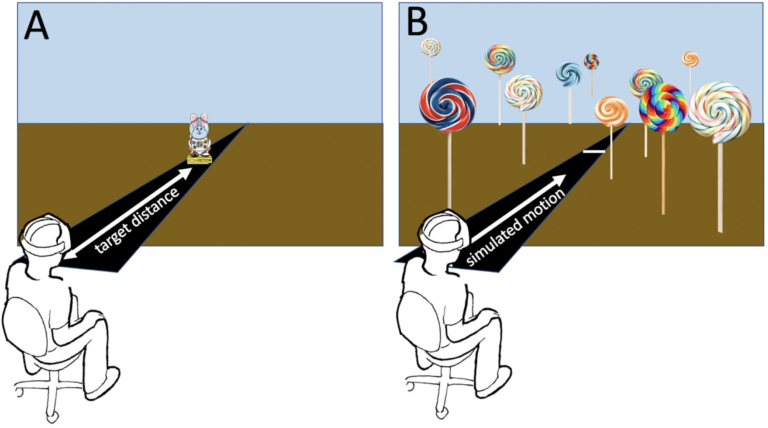
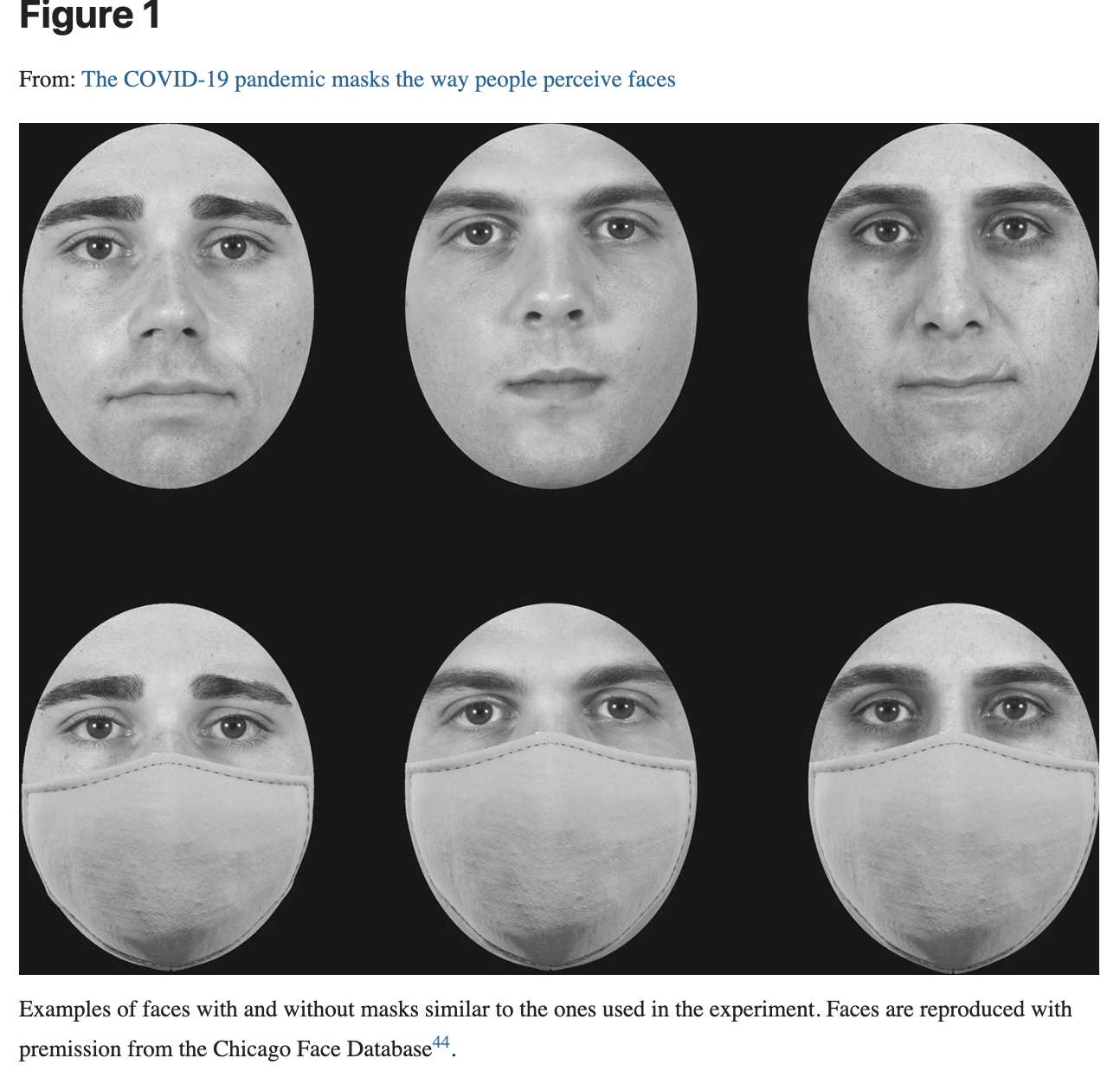
The Centre for Vision Research (CVR) at York University pursues world-class, interdisciplinary research and training in visual science and its applications. The CVR brings together researchers from psychology, electrical engineering & computer science, biology, physics, digital media, philosophy, kinesiology & health science, and other disciplines in a highly interdisciplinary and collaborative centre. Fundamental research that merges techniques in human psychophysics, visual neuroscience, computer vision and computational theory is supported by leading-edge facilities including a 3T fMRI scanner, neurophysiological and neural stimulation suites, immersive projection virtual reality displays, and a wide array of visuo-robotic platforms.
The Centre for Vision Research is the foundation for York’s Vision Science to Applications (VISTA) program funded by the Canada First Research Excellence Fund (CFREF, 2016-2023). VISTA is an ambitious collaborative program that builds on and extends York’s world-leading interdisciplinary expertise in biological and computer vision. Most CVR members are associated with VISTA and the project provides significant resources and opportunities for CVR faculty, researchers, students, and partners.
CVR - VISTA conference: New VISTAs in Vision Research
December 4 - 7, 2023
York University, Toronto
CVR Events

Babies Are Born with an Innate Number Sense.
Plato was right: newborns do math
Watch Graham Wakefield's fascinating presentation on Computational Worldmaking at Virtual Reality Toronto (2021)

Training Opportunities
Explore how you can join the CVR as a postdoc, graduate student or undergraduate student

CVR Members
Get familiar with the CVR researchers, their research areas, laboratories and interests

Resources
Learn about the unique set of research resources that we use to study vision